目标检测任务的损失函数由Classificition Loss(分类损失)和Regeression Loss(回归损失)两部分构成。
目标检测任务中损失函数的大致演变过程按照时间线可以划分如为Smooth L1 Loss->IoU Loss-> GIoU Loss -> DIoU Loss ->CIoU Loss。本文将简单介绍集中IOU损失函数 详细的介绍欢迎阅读全文:
IOU 损失函数
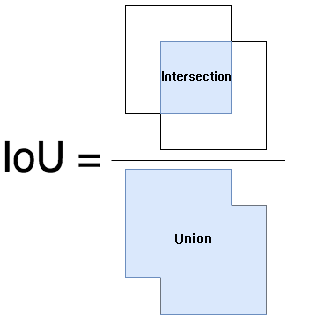
IOU 就是常说的交并比
$$IoU=\frac{|A \cap B|}{|A \cup B|}$$
$$IoULoss = -ln(\frac{|A \cap B|}{|A \cup B|})$$
- 优点
- 它可以真实的反映预测框的检测效果。
- 还有一个特性就是尺度不变性,也就是对尺度不敏感(scale invariant), 在regression任务中,判断predict box和atrget box的距离最直接的指标就是IoU。**(满足非负性;同一性;对称性;三角不等性)**
- IOU 的缺点
- 如果两个框没有相交,根据定义,IoU=0,不能反映两者的距离大小(重合度)。同时因为loss=0,没有梯度回传,无法进行学习训练。
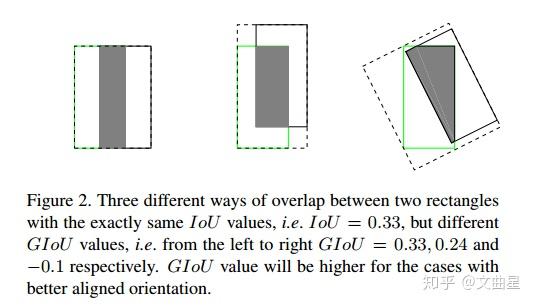
- IoU无法精确的反映两者的重合度大小。如下图所示,三种情况IoU都相等,但看得出来他们的重合度是不一样的,左边的图回归的效果最好,右边的最差。
GIOU
$$G I o U=I o U-\frac{\left|A_{c}-U\right|}{\left|A_{c}\right|}$$
上面公式的意思是:先计算两个框的最小闭包区域面积$A_c$(通俗理解:**同时包含了预测框和真实框**的最小框的面积),再计算出IoU,再计算闭包区域中不属于两个框的区域占闭包区域的比重,最后用IoU减去这个比重得到GIoU
$$L_{GIOU} = 1-GIOU$$
- 优点
- GIoU对scale不敏感
- GIoU是IoU的下界,在两个框无限重合的情况下,IoU=GIoU=1
- IoU取值[0,1],但GIoU有对称区间,取值范围[-1,1]。在两者重合的时候取最大值1,在两者无交集且无限远的时候取最小值-1,因此GIoU是一个非常好的距离度量指标。
- 与IoU只关注重叠区域不同,GIoU不仅关注重叠区域,还关注其他的非重合区域,能更好的反映两者的重合度。
- GIoU Loss不足
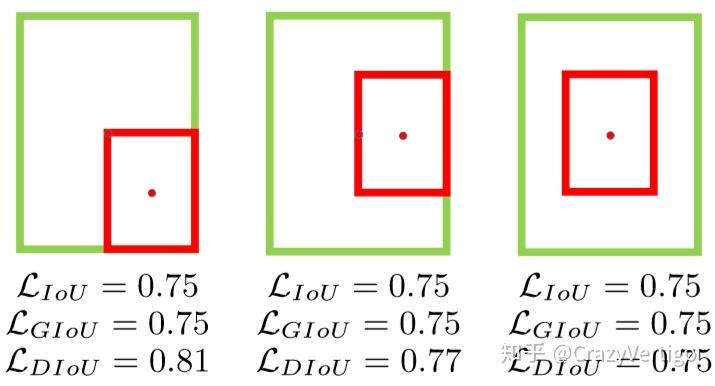
当目标框完全包裹预测框的时候,IoU和GIoU的值都一样,此时GIoU退化为IoU。
DIOU
好的目标框回归损失应该考虑三个重要的几何因素:
重叠面积,中心点距离,长宽比。
基于IoU和GIoU存在的问题,作者提出了两个问题:
- 直接最小化anchor框与目标框之间的归一化距离是否可行,以达到更快的收敛速度?
- 如何使回归在与目标框有重叠甚至包含时更准确、更快?
基于问题一,作者提出了DIoU Loss,相对于GIoU Loss收敛速度更快,该Loss考虑了重叠面积和中心点距离,但没有考虑到长宽比;
针对问题二,作者提出了CIoU Loss,其收敛的精度更高,以上三个因素都考虑到了。
通常基于IoU-based的loss可以定义为 $L=1-I o U+R\left(B, B^{g t}\right)$ ,其中 $R\left(B, B^{g t}\right)$ 定义为预测框 $B$和目标框 $B^{gt}$的惩罚项。
- DIoU中的惩罚项表示为 $R_{D I o U}=\frac{\rho^{2}\left(b, b^{g t}\right)}{c^{2}}$,其中 $b$和$b^{gt}$ 分别表示 $B$和$B^{gt}$ 的中心点, $\rho(\cdot)$表示欧式距离, $c$表示 $B$和$B^{gt}$的最小外界矩形的对角线距离,如下图所示。可以将DIoU替换IoU用于NMS算法当中,也即论文提出的DIoU-NMS,实验结果表明有一定的提升。
- DIoU Loss function定义为:
$$L_{D I o U}=1-I o U+\frac{\rho^{2}\left(b, b^{g t}\right)}{c^{2}}$$
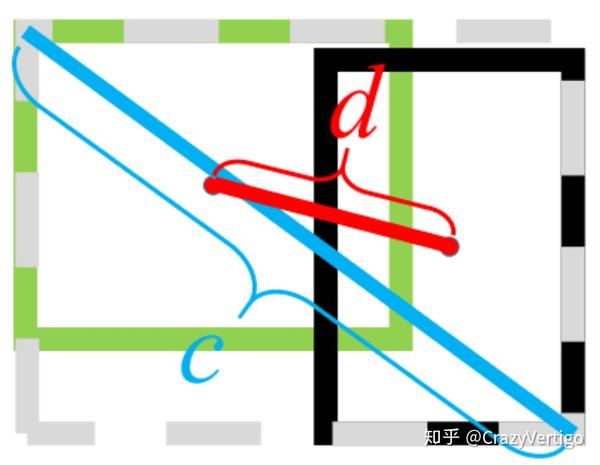
绿色框为目标框,黑色框为预测框,灰色框为两者的最小外界矩形框,d表示目标框和真实框的中心点距离,c表示最小外界矩形框的距离。
- 优点
- 尺度不变性
- 当两个框完全重合时, $L_{IOU} = L_{GIOU} = L{DIOU} = 0$ ,当2个框不相交时$L_{G I o U}=L_{D I o U} \rightarrow 2$
- DIoU Loss可以直接优化2个框直接的距离,比GIoU Loss收敛速度更快
- 对于目标框包裹预测框的这种情况,DIoU Loss可以收敛的很快,而GIoU Loss此时退化为IoU Loss收敛速度较慢
CIOU
Complete-IoU Loss
CIoU的惩罚项是在DIoU的惩罚项基础上加了一个影响因子 $\alpha v$ ,这个因子把预测框长宽比拟合目标框的长宽比考虑进去。
$$R_{C I o U}=\frac{\rho^{2}\left(b, b^{g t}\right)}{c^{2}}+\alpha v$$
其中 $\alpha$是用于做trade-off的参数, $\alpha = \frac{v}{(1-I o U)+v}$, $v$是用来衡量长宽比一致性的参数,定义为
$$v=\frac{4}{\pi^{2}}\left(\arctan \frac{w^{g t}}{h^{g t}}-\arctan \frac{w}{h}\right)^{2}$$
CIoU Loss function的定义为
$$L_{CIoU} = 1-IoU + \frac{\rho^2(b,b^{gt})}{c^2}+\alpha v$$

