Batchnorm原理详解
前言:Batchnorm是深度网络中经常用到的加速神经网络训练,加速收敛速度及稳定性的算法,可以说是目前深度网络必不可少的一部分。
本文旨在用通俗易懂的语言,对深度学习的常用算法–batchnorm的原理及其代码实现做一个详细的解读。本文主要包括以下几个部分。
- Batchnorm主要解决的问题
- Batchnorm原理解读
- Batchnorm的优点
- Batchnorm的源码解读
第一节:Batchnorm主要解决的问题
首先,此部分也即是讲为什么深度网络会需要batchnorm
,我们都知道,深度学习的话尤其是在CV上都需要对数据做归一化,因为深度神经网络主要就是为了学习训练数据的分布,并在测试集上达到很好的泛化效果,但是,如果我们每一个batch输入的数据都具有不同的分布,显然会给网络的训练带来困难。另一方面,数据经过一层层网络计算后,其数据分布也在发生着变化,此现象称为Internal Covariate Shift,接下来会详细解释,会给下一层的网络学习带来困难。batchnorm
直译过来就是批规范化,就是为了解决这个分布变化问题。
1.1 Internal Covariate Shift
Internal
Covariate Shift :此术语是google小组在论文Batch Normalizatoin 中提出来的,其主要描述的是:训练深度网络的时候经常发生训练困难的问题,因为,每一次参数迭代更新后,上一层网络的输出数据经过这一层网络计算后,数据的分布会发生变化,为下一层网络的学习带来困难(神经网络本来就是要学习数据的分布,要是分布一直在变,学习就很难了),此现象称之为Internal Covariate Shift
。
Batch
Normalizatoin
之前的解决方案就是使用较小的学习率,和小心的初始化参数,对数据做白化处理,但是显然治标不治本。
1.2 covariate shift
Internal
Covariate Shift 和Covariate Shift具有相似性,但并不是一个东西,前者发生在神经网络的内部,所以是Internal,后者发生在输入数据上。Covariate Shift
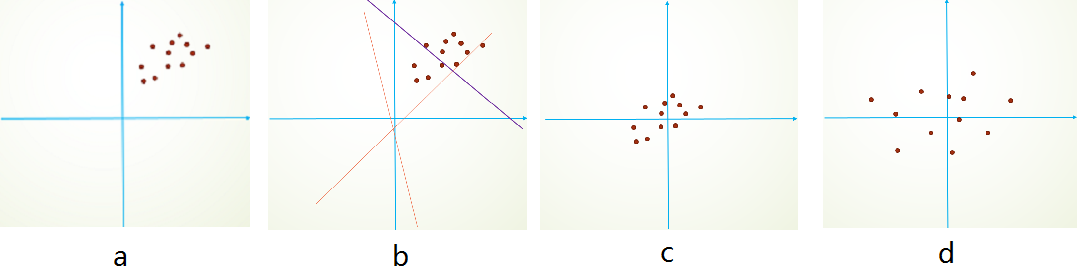
主要描述的是由于训练数据和测试数据存在分布的差异性,给网络的泛化性和训练速度带来了影响,我们经常使用的方法是做归一化或者白化。想要直观感受的话,看下图:
举个简单线性分类栗子,假设我们的数据分布如a所示,参数初始化一般是0均值,和较小的方差,此时拟合的y=wx+b
如b图中的橘色线,经过多次迭代后,达到紫色线,此时具有很好的分类效果,但是如果我们将其归一化到0点附近,显然会加快训练速度,如此我们更进一步的通过变换拉大数据之间的相对差异性,那么就更容易区分了。
Covariate
Shift 就是描述的输入数据分布不一致的现象,对数据做归一化当然可以加快训练速度,能对数据做去相关性,突出它们之间的分布相对差异就更好了。Batchnorm做到了,前文已说过,Batchnorm是归一化的一种手段,极限来说,这种方式会减小图像之间的绝对差异,突出相对差异,加快训练速度。所以说,并不是在深度学习的所有领域都可以使用BatchNorm
,下文会写到其不适用的情况。
第二节:Batchnorm 原理解读
本部分主要结合原论文部分,排除一些复杂的数学公式,对BatchNorm
的原理做尽可能详细的解释。
之前就说过,为了减小Internal
Covariate Shift,对神经网络的每一层做归一化不就可以了,假设将每一层输出后的数据都归一化到0均值,1方差,满足正太分布,但是,此时有一个问题,每一层的数据分布都是标准正太分布,导致其完全学习不到输入数据的特征,因为,费劲心思学习到的特征分布被归一化了,因此,直接对每一层做归一化显然是不合理的。
但是如果稍作修改,加入可训练的参数做归一化,那就是BatchNorm
实现的了,接下来结合下图的伪代码做详细的分析:
之所以称之为batchnorm是因为所norm的数据是一个batch的,假设输入数据是β=x1…m
共m个数据,输出是yi=BN(x),batchnorm
的步骤如下:
1.先求出此次批量数据x
的均值,μβ=1m∑mi=1xi
2.求出此次batch的方差,σ2β=1m∑i=1m(xi−μβ)2
3.接下来就是对x做归一化,得到x−i
4.最重要的一步,引入缩放和平移变量γ和β ,计算归一化后的值,yi=γx−i +β
接下来详细介绍一下这额外的两个参数,之前也说过如果直接做归一化不做其他处理,神经网络是学不到任何东西的,但是加入这两个参数后,事情就不一样了,先考虑特殊情况下,如果γ
和β分别等于此batch的方差和均值,那么yi不就还原到归一化前的x了吗,也即是缩放平移到了归一化前的分布,相当于batchnorm没有起作用,β 和γ
分别称之为 平移参数和缩放参数 。这样就保证了每一次数据经过归一化后还保留的有学习来的特征,同时又能完成归一化这个操作,加速训练。
先用一个简单的代码举个小栗子:
def Batchnorm_simple_for_train(x, gamma, beta, bn_param):"""param:x : 输入数据,设shape(B,L)param:gama : 缩放因子 γparam:beta : 平移因子 βparam:bn_param : batchnorm所需要的一些参数 eps : 接近0的数,防止分母出现0 momentum : 动量参数,一般为0.9, 0.99, 0.999 running_mean :滑动平均的方式计算新的均值,训练时计算,为测试数据做准备 running_var : 滑动平均的方式计算新的方差,训练时计算,为测试数据做准备""" running_mean = bn_param['running_mean'] #shape = [B] running_var = bn_param['running_var'] #shape = [B] results = 0. # 建立一个新的变量 x_mean=x.mean(axis=0) # 计算x的均值 x_var=x.var(axis=0) # 计算方差 x_normalized=(x-x_mean)/np.sqrt(x_var+eps) # 归一化 results = gamma * x_normalized + beta # 缩放平移 running_mean = momentum * running_mean + (1 - momentum) * x_mean running_var = momentum * running_var + (1 - momentum) * x_var #记录新的值 bn_param['running_mean'] = running_mean bn_param['running_var'] = running_var return results , bn_param看完这个代码是不是对batchnorm有了一个清晰的理解,首先计算均值和方差,然后归一化,然后缩放和平移,完事!但是这是在训练中完成的任务,每次训练给一个批量,然后计算批量的均值方差,但是在测试的时候可不是这样,测试的时候每次只输入一张图片,这怎么计算批量的均值和方差,于是,就有了代码中下面两行,在训练的时候实现计算好mean
var
测试的时候直接拿来用就可以了,不用计算均值和方差。
running_mean = momentum * running_mean + (1 - momentum) * x_meanrunning_var = momentum * running_var + (1 - momentum) * x_var所以,测试的时候是这样的:
def Batchnorm_simple_for_test(x, gamma, beta, bn_param):"""param:x : 输入数据,设shape(B,L)param:gama : 缩放因子 γparam:beta : 平移因子 βparam:bn_param : batchnorm所需要的一些参数 eps : 接近0的数,防止分母出现0 momentum : 动量参数,一般为0.9, 0.99, 0.999 running_mean :滑动平均的方式计算新的均值,训练时计算,为测试数据做准备 running_var : 滑动平均的方式计算新的方差,训练时计算,为测试数据做准备""" running_mean = bn_param['running_mean'] #shape = [B] running_var = bn_param['running_var'] #shape = [B] results = 0. # 建立一个新的变量 x_normalized=(x-running_mean )/np.sqrt(running_var +eps) # 归一化 results = gamma * x_normalized + beta # 缩放平移 return results , bn_param你是否理解了呢?如果还没有理解的话,欢迎再多看几遍。
第三节:Batchnorm源码解读
本节主要讲解一段tensorflow中Batchnorm
的可以使用的代码3
,如下:
代码来自知乎,这里加入注释帮助阅读。
def batch_norm_layer(x, train_phase, scope_bn): with tf.variable_scope(scope_bn): # 新建两个变量,平移、缩放因子 beta = tf.Variable(tf.constant(0.0, shape=[x.shape[-1]]), name='beta', trainable=True) gamma = tf.Variable(tf.constant(1.0, shape=[x.shape[-1]]), name='gamma', trainable=True) # 计算此次批量的均值和方差 axises = np.arange(len(x.shape) - 1) batch_mean, batch_var = tf.nn.moments(x, axises, name='moments') # 滑动平均做衰减 ema = tf.train.ExponentialMovingAverage(decay=0.5) def mean_var_with_update(): ema_apply_op = ema.apply([batch_mean, batch_var]) with tf.control_dependencies([ema_apply_op]): return tf.identity(batch_mean), tf.identity(batch_var) # train_phase 训练还是测试的flag # 训练阶段计算runing_mean和runing_var,使用mean_var_with_update()函数 # 测试的时候直接把之前计算的拿去用 ema.average(batch_mean) mean, var = tf.cond(train_phase, mean_var_with_update, lambda: (ema.average(batch_mean), ema.average(batch_var))) normed = tf.nn.batch_normalization(x, mean, var, beta, gamma, 1e-3) return normed至于此行代码tf.nn.batch_normalization()就是简单的计算batchnorm过程啦,代码如下:
这个函数所实现的功能就如此公式:γ(x−μ)σ+β
def batch_normalization(x, mean, variance, offset, scale, variance_epsilon, name=None): with ops.name_scope(name, "batchnorm", [x, mean, variance, scale, offset]): inv = math_ops.rsqrt(variance + variance_epsilon) if scale is not None: inv *= scale return x * inv + (offset - mean * inv if offset is not None else -mean * inv)第四节:Batchnorm的优点
主要部分说完了,接下来对BatchNorm做一个总结:
- 没有它之前,需要小心的调整学习率和权重初始化,但是有了BN可以放心的使用大学习率,但是使用了BN,就不用小心的调参了,较大的学习率极大的提高了学习速度,
- Batchnorm本身上也是一种正则的方式,可以代替其他正则方式如dropout等
- 另外,个人认为,batchnorm降低了数据之间的绝对差异,有一个去相关的性质,更多的考虑相对差异性,因此在分类任务上具有更好的效果。
注:或许大家都知道了,韩国团队在2017NTIRE图像超分辨率中取得了top1的成绩,主要原因竟是去掉了网络中的batchnorm层,由此可见,BN并不是适用于所有任务的,在image-to-image这样的任务中,尤其是超分辨率上,图像的绝对差异显得尤为重要,所以batchnorm的scale并不适合。
参考文献:
【1】 http://blog.csdn.net/zhikangfu/article/details/53391840
【2】 http://geek.csdn.net/news/detail/160906
【3】 https://www.zhihu.com/question/53133249